Where Is 23pi/6 on the Unit Circle

Sec π 6 sec π 6 The exact value of secπ 6 sec π 6. The cosine function is positive in the 4th quadrant.

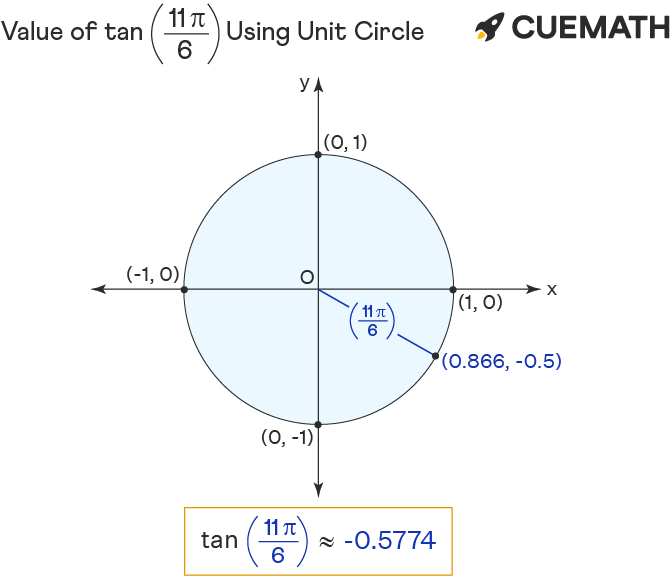
Tan 11pi 6 Find Value Of Tan 11pi 6 Tan 11p 6

Since sine is an odd function the value of sin-11pi6 -sin11pi6.

. The value of tan 11pi6 can be calculated by constructing an angle of 11π6 radians with the x-axis and then finding the coordinates of the corresponding point 0866 -05 on the unit circle. 23π 6 - 23 π 6. Tap for more steps.

Where in our case is the terminal side of the angle in standard position. Sec 11π 6 sec 11 π 6 Apply the reference angle by finding the angle with equivalent trig values in the first quadrant. Is the required point.

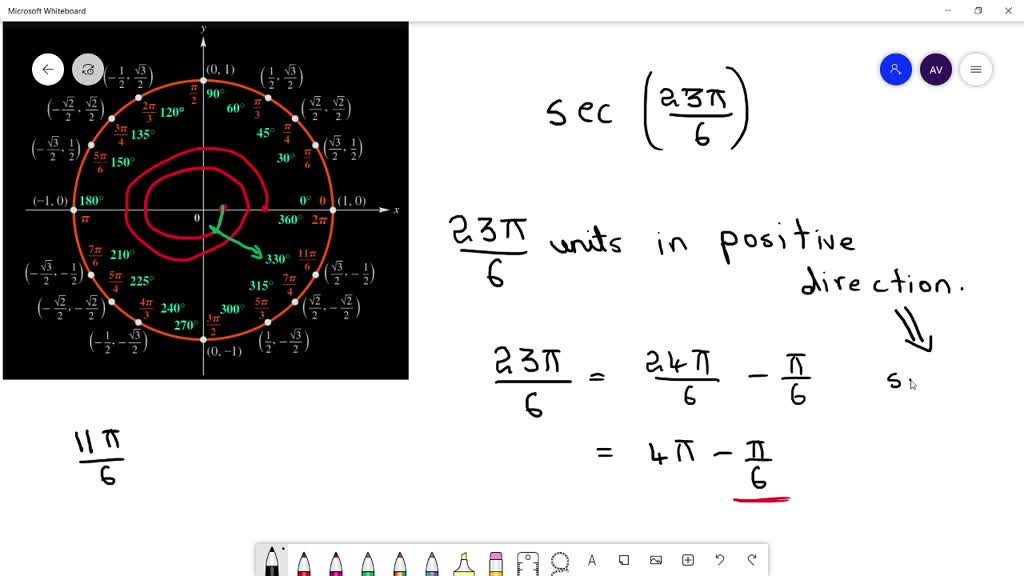
Therefore we conclude that sec23π6 233. Convert from Radians to Degrees 13pi6. X y - 4 -2x 3y 6 Solve each system by equation.

See this page for the modern version of the chart. This site uses the circle constant τ tau instead of π pi when measuring angles in radians. Find the Exact Value sec 23pi6 sec 23π 6 sec 23 π 6 Remove full rotations of 2π 2 π until the angle is between 0 0 and 2π 2 π.

This page exists to match what is taught in schools. Tap for more steps. Factor π π out of 13 π 13 π.

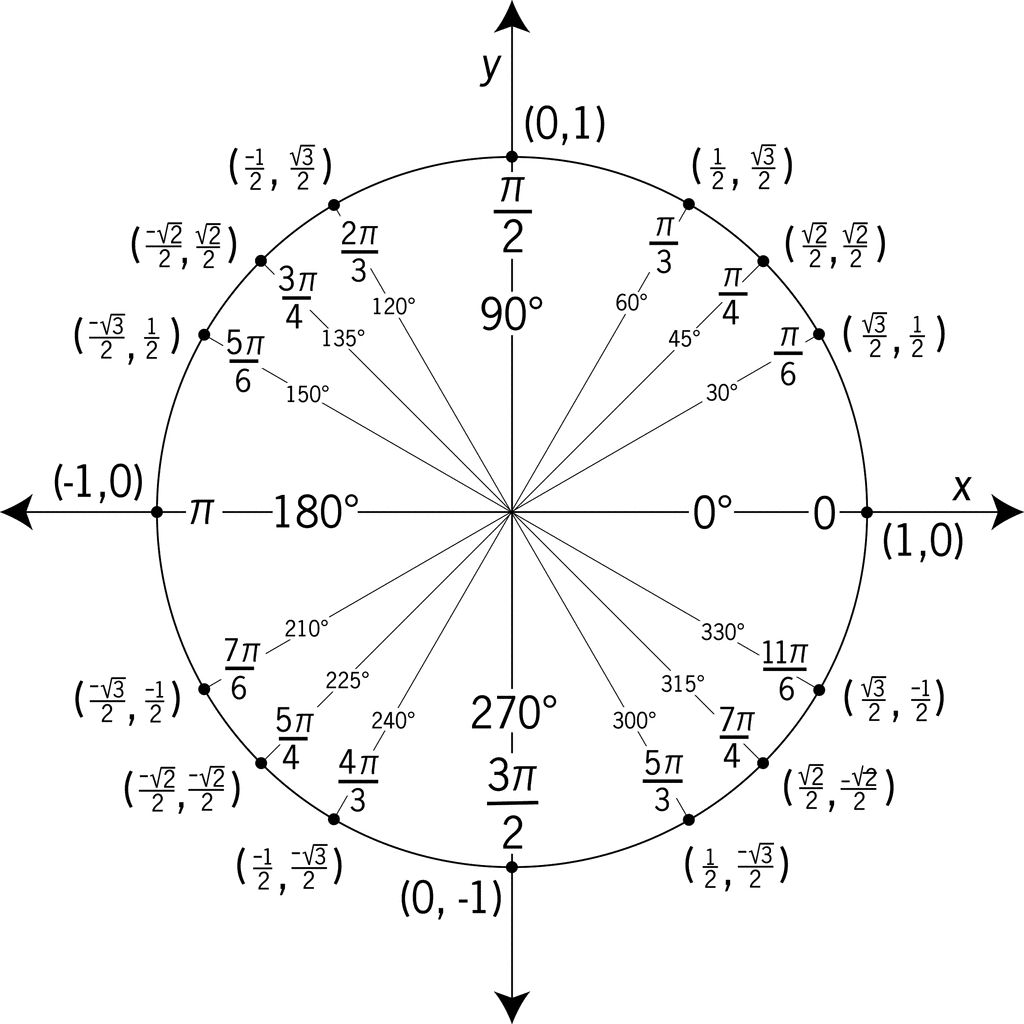
The first one is by radians and the second one is by degrees. The unit circle has the parametric equation. To convert radians to degrees multiply by 180 π 180 π since a full circle is 360 360 or 2π 2 π radians.

Unit Circle Chart π pi The unit circle chart shows the position of the points on the unit circle that are formed by dividing the circle into eight and twelve equal parts. The sine function is negative in the 4th quadrant. So youre just looking at π 6.

Methods to Find Value of Sin 11pi6. This problem has been solved. Sec23pi6 I know the answer should be.

The value of sin 11pi6 is given as -05. On the trig unit circle sin 19π 6 sin 7π 6 12π 6 sin 7π 6 2π. Convert the radian measure to degrees.

The unit circle chart shows the position of the points on the unit circle that are formed by dividing the circle into equal parts. Find the Quadrant of the Angle - 23pi6. Cos 11pi6 cos 23pi6 cos 35pi6 and so on.

Tan 11pi6 -13 or -05774. Angles in the unit circle can be written in two ways. Tap for more steps.

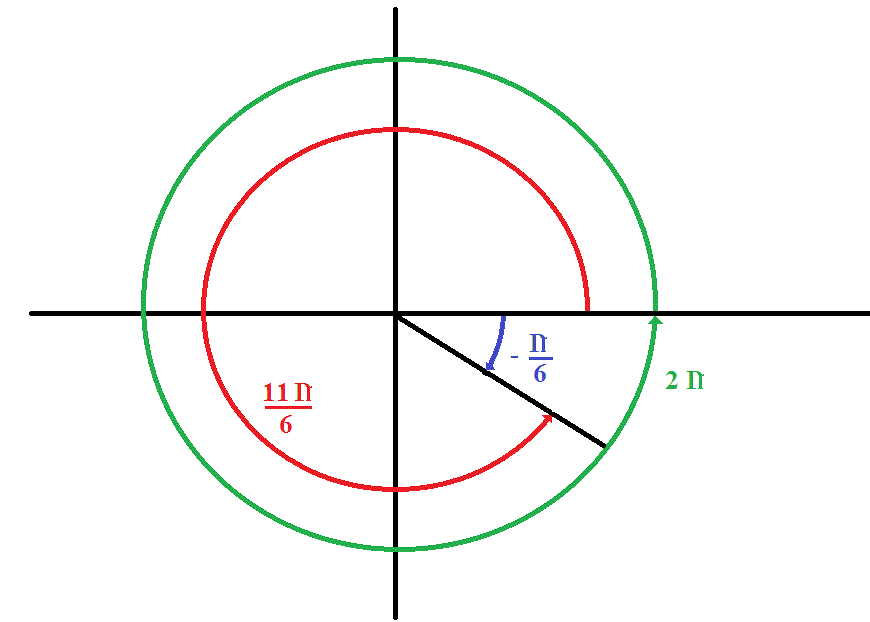
Notice that 25π 6 24 1π 6 4π π 6. Subtract full rotations of until the angle is greater than or equal to and less than. Evaluate cos 23pi6 cos 23π 6 cos 23 π 6 Remove full rotations of 2π 2 π until the angle is between 0 0 and 2π 2 π.

We know for a fact that a unit circle measures 2π 360 2 π 360 and. 2sqrt33 but I do not understand how to solve the problem. We can find the value of sin 11pi6 by.

We substitute to get. Find the value of cos dfrac23pi 6 using the unit. Trig unit circle and trig table -- sin 23pi6 sin -pi6 24pi6 sin -pi6 4pi sin -pi6 - sin pi6 - 12 Unit circle and property.

Advertisement Advertisement New questions in Mathematics. I have a unit circle but 23pi6 is not on it so I dont know how to find the xy Pre Calculus. Let θ be an.

We can subtract 2π from 19π 6 and still have the same value of cosine--the angles would be in the same location in the unit circle. The reference angle for 11π6 is π6 because it is the difference from 2π. Cancel the common factor of π π.

Find the Value Using the Unit Circle 13pi6. See the answer See the answer See the answer done loading. Tap for more steps.

We can find the value of cos 11pi6 by. π 13 6 180 π π 13 6. Since cosine is negative in QIII.

Find the reference number r for the point Pt on the unit circle for each given value of t below A t 5PI4 B t 23PI6 C t -8PI5. Since cosine is an even function the value of cos-11pi6 cos11pi6. You can ignore the 2 full cycles of 2π.

Sin π 6 1 2. 23 π 6 180 π - 23 π 6. Notice that 7π 6 π π 6 so this angle is in QIII and has a reference angle of π 6.

Sin 11pi6 sin 23pi6 sin 35pi6 and so on. 13π 6 13 π 6. 19π 6 2π 19π 6 12π 6 7π 6.

13π 6 180 π 13 π 6 180 π. Sin π 6 1 2. The angles on the charts shown on this page are measured in radians.

Cos 11π 6 cos 11 π 6 Apply the reference angle by finding the angle with equivalent trig values in the first quadrant. The value of cos 11pi6 is given as 086602. The value of tan 11pi6 is equal to the y-coordinate -05 divided by the x-coordinate 0866.

See the unit circle chart annotated with π. Methods to Find Value of Cos 11pi6. The value of sec23π6 is secπ6 1cosπ6 132 233 To determine the sign of the value we know that the angle 5π6 lies in the fourth quadrant where the value of cosine is positive.

To convert radians to degrees multiply by 180 π 180 π since a full circle is 360 360 or 2 π 2 π radians. Find the exact circular function value for. Thus cos 19π 6 cos7π 6.

Subtract full rotations of until the angle is greater than or equal to and less than. Cos π 6 cos π 6. The exact value of is.

Content Radian Measure

Let S Learn The Unit Circle Angles In Standard Position Arc Length

How Do You Find The Coordinates Of The Terminal Points Corresponding To The Following Arc Length On The Unit Circle 11p 6 Socratic

How Do You Find The Exact Value Of Cos 19pi 6 Socratic

Solved Find Each Exact Function Value Sec Frac 23 Pi 6

Ex Sine And Cosine Values Using The Unit Circle Multiples Of Pi 6 Radians Youtube

How To Draw An Angle Between 0 And 2pi In Standard Position Given An Angle In Radians Trigonometry Study Com

Trigonometry Finding The Exact Value Of Cot 23p 4 Using Unit Circle Mathematics Stack Exchange

Unit Circle Definition Of Trigonometric Functions Trig Functions Trigonometric Functions Circle Definition Unit Circle Radians

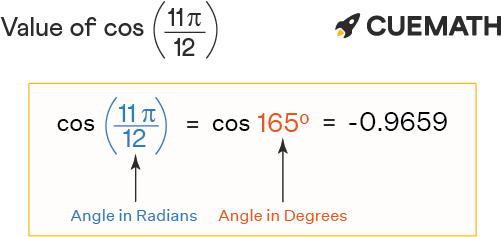
Cos 11pi 12 Find Value Of Cos 11pi 12 Cos 11p 12

Unit Circle Labeled With Special Angles And Values Clipart Etc How To Memorize Things Trigonometry Math Formulas

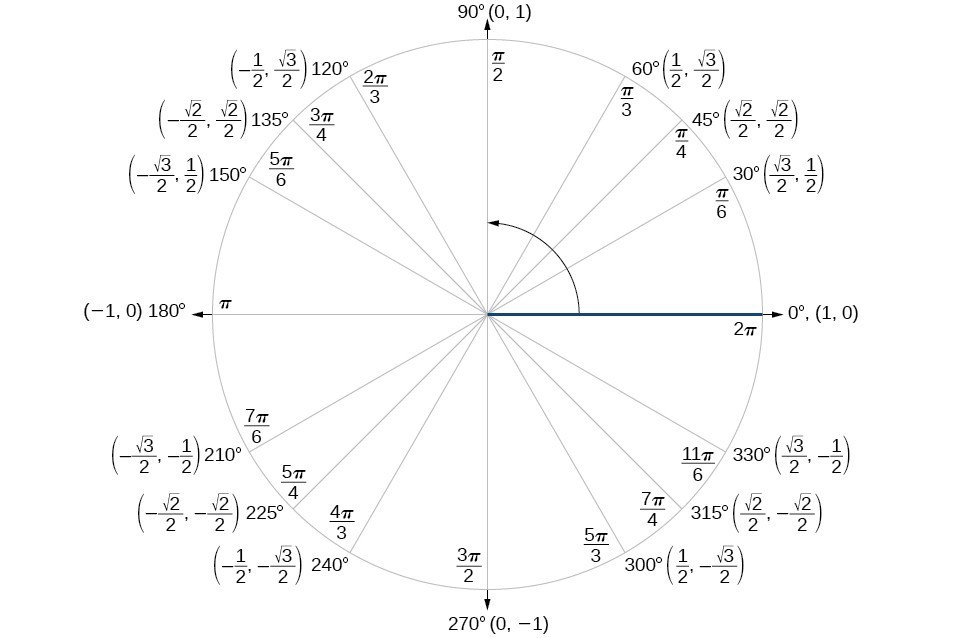
Sum And Difference Identities Precalculus Ii

Interaction Between Particles With Inhomogeneous Surface Charge Distributions Revisiting The Coulomb Fission Of Dication Molecular Clusters The Journal Of Chemical Physics Vol 151 No 15

Unit Circle Definition Of Trigonometric Functions Trig Functions Trigonometric Functions Circle Definition Unit Circle Radians

The Unit Circle Ck 12 Foundation

Trigonometry

The Unit Circle Ck 12 Foundation

23pi 6 Radians In Degrees All Information Best Calculator More

Where Is 23pi 6 On The Unit Circle Study Com